Last year my son took pre-calc at the community college and had trouble with radians and related work. I didn't have any clue, so I could not really help him too much...but now I've learned what they are and it's so easy!!
What is a radian? Basically pi radians = 180 degrees. So to transform between degrees and radians, you just use the fraction 180°/π radians or π radians/180°
so for example, if you would like to see how many radians is 74° ?
well, 74° * π radians/180°, so that'd give you 1.2915 radians
hmmm....
well, applying all of that to geometry/trigonometry type stuff...
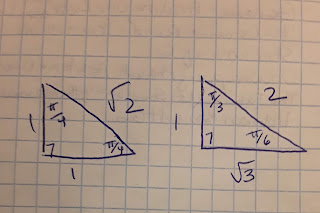
you will see that 30° equals π/6 and 60° equals π/3 and 45 ° equals π/4 and then you can use your triangle rules for a 30-60-90 triangle proportions, where the side opposite the 30 would be 1, the side opposite the 60 is √3 and the hypotenuse is then 2. You can easily do the sines/cosines/tangents etc using this triangle. And for the 45-45-90 triangle you can use the π/4 relationship as well:

No comments:
Post a Comment